
Handling cyclical features, such as hours in a day, for machine learning pipelines with Python example
2021-03-26
Python __getattr__ and __getattribute__ magic methods
2021-06-06Consider a two-dimensional data set consisting of 5 rows and 7 columns, where each element contains a value. Such data is commonly referred to as a matrix, and in this case, it is a dense 5 x 7 matrix. However, if only a few elements of the matrix have non-zero values, storing the data in a two-dimensional structure is wasteful, particularly when the data’s dimensions are large.
To address this issue, sparse matrices provide a memory-efficient data structure for storing large matrices with minimal non-zero elements. Not only does this structure allow for efficient storage, but it also enables complex matrix computations, making it a powerful tool in many data science problems. Developing the ability to work with sparse matrices, large matrices, or two-dimensional arrays with numerous zero elements can be incredibly beneficial.
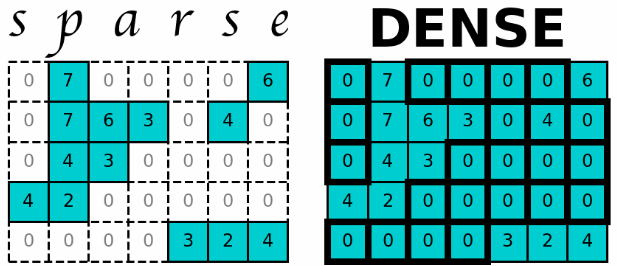
Python’s SciPy library has a lot of options for creating, storing, and operating with Sparse matrices. There are 7 different types of sparse matrices available.
- bsr_matrix: Block Sparse Row matrix
- coo_matrix: COOrdinate format matrix
- csc_matrix: Compressed Sparse Column matrix
- csr_matrix: Compressed Sparse Row matrix
- dia_matrix: Sparse matrix with DIAgonal storage
- dok_matrix: Dictionary Of Keys based sparse matrix.
- lil_matrix: Row-based linked list sparse matrix
Selecting the right sparse matrix
Each of the sparse matrices excels in specific operations in terms of efficiency and speed. For instance, lil_matrix or dok_matrix are efficient when constructing a new sparse matrix from scratch, while coo_matrix is useful for creating a sparse matrix but not for operations. On the other hand, when it comes to matrix operations such as multiplication or inversion, the CSC or CSR sparse matrix format is more suitable and efficient. The csc_matrix has faster column slicing, while the csr_matrix has faster row slicing, owing to the data structure. The choice of the appropriate sparse matrix depends on the application and may require multiple formats to achieve the desired outcome. The SciPy’s sparse module offers excellent functions for converting one sparse matrix type to another.
Creating a COO sparse matrix
The COO (COOrdinate) sparse matrix is among the more straightforward matrices to work with. Creating a COO sparse matrix is a fast process that requires the coordinates of the non-zero elements in the sparse matrix. To create a coo_matrix, we need three one-dimensional NumPy arrays: the first array contains row indices, the second array contains column indices, and the third array contains non-zero data in the element. The row and column indices specify the location of the non-zero element, while the data array contains the actual non-zero data.
Let us create a sparse matrix in a COO format using a simple example. Let us first create 3 NumPy arrays needed to create the COO sparse matrix.
# import sparse module from SciPy package
from scipy import sparse
# import uniform module to create random numbers
from scipy.stats import uniform
# import NumPy
import numpy as np
# row indices
row_ind = np.array([0, 1, 1, 3, 4])
# column indices
col_ind = np.array([0, 2, 4, 3, 4])
# data to be stored in COO sparse
matrixdata = np.array([1, 2, 3, 4, 5], dtype=float)
We can use sparse.coo_matrix to create a sparse matrix in COO format. It takes data and the row and column index tuple as arguments.
# create COO sparse matrix from three arrays
mat_coo = sparse.coo_matrix((data, (row_ind, col_ind)))
# print coo_matrix
print(mat_coo)
(0, 0) 1.0
(1, 2) 2.0
(1, 4) 3.0
(3, 3) 4.0
(4, 4) 5.0
coo_matrix has lots of useful functions including a function to convert coo_matrix to other sparse matrices and also to dense matrices. Here is a function toarray to see the 2D array of the sparse matrix that we just created.
print(mat_coo.toarray())
[[ 1. 0. 0. 0. 0.]
[ 0. 0. 2. 0. 3.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 4. 0.]
[ 0. 0. 0. 0. 5.]]
Here is an example to convert a coo matrix to CSC sparse matrix.
print(mat_coo.tocsc())
(0, 0) 1.0
(1, 2) 2.0
(3, 3) 4.0
(1, 4) 3.0
(4, 4) 5.0
Note the order of data stored in CSC format is different from the COO sparse matrix.
Creating a sparse matrix from a dense (full) matrix
it is often the case that we start with a full matrix as input. Here is an example of how to create a sparse matrix using an existing 2D array/matrix. This time, we will create a csr_matrix sparse matrix and populate it with random numbers from a uniform distribution in SciPy.stats. To reproduce the same random numbers, we will first set a seed for random number generation. We will create a toy sparse matrix with only four rows and four columns by first generating uniform random numbers from 0 to 2 in a 1D NumPy array, and then reshaping it using the reshape function to create a 2D NumPy array, which is a matrix.
np.random.seed(seed=42)
data = uniform.rvs(size=16, loc = 0, scale=2)
data = np.reshape(data, (4, 4))
data
We can see that we have created a 4×4 2d array with uniform random numbers.
array([[ 0.74908024, 1.90142861, 1.46398788, 1.19731697],
[ 0.31203728, 0.31198904, 0.11616722, 1.73235229],
[ 1.20223002, 1.41614516, 0.04116899, 1.9398197 ],
[ 1.66488528, 0.42467822, 0.36364993, 0.36680902]])
Let us convert this full matrix into a sparse matrix. Let us first make some of the elements of matrix zero. Here any element with values less than 1 will be assigned to 0. Now half the elements of this matrix are zero.
# make elements with value less < 1 to zero
data[data < 1] = 0
We can see that elements with values less than 1 are zero now.
data
array([[ 0. , 1.90142861, 1.46398788, 1.19731697],
[ 0. , 0. , 0. , 1.73235229],
[ 1.20223002, 1.41614516, 0. , 1.9398197 ],
[ 1.66488528, 0. , 0. , 0. ]])
Now we convert this full matrix with zeroes to a sparse matrix using the sparse module in SciPy. As you just saw, SciPy has multiple options for sparse matrices. We will be using csr_matrix, where CSR stands for Compressed Sparse Row.
data_csr = sparse.csr_matrix(data)
We can also print the small sparse matrix to see how the data is stored.
print(data_csr)
(0, 1) 1.90142861282
(0, 2) 1.46398788362
(0, 3) 1.19731696839
(1, 3) 1.73235229155
(2, 0) 1.20223002349
(2, 1) 1.41614515559
(2, 3) 1.93981970432
(3, 0) 1.6648852816
We can see that in the CSR sparse matrix, we have only nonzero elements. Also, the elements are stored row-wise, leaving zero elements. The toy example showed how to create a sparse matrix from a full matrix in Python.
Space saved by a big sparse matrix
One of the real uses of sparse matrices is the huge space reduction to store sparse matrices. Let us create a bigger full matrix using uniform random numbers.
np.random.seed(seed=42)
data = uniform.rvs(size=1000000, loc = 0, scale=2)
data = np.reshape(data, (10000, 100))
Let us make the matrix sparse by making certain elements zero. As before, we make any element whose value is less than 1 to 0. We can use nbytes function in NumPy to get the number of bytes and get the size of the matrix in MB.
data[data < 1] = 0 >data_size = data.nbytes/(1024**2)
>print('Size of full matrix with zeros: '+ '%3.2f' %data_size + ' MB')
Size of full matrix with zeros: 76.29 MB
We can see the size of the full matrix of size 1 Million elements with half of them with values of zero is about 80 MB.
data_csr = sparse.csr_matrix(data)
data_csr_size = data_csr.data.size/(1024**2)
print('Size of sparse csr_matrix: '+ '%3.2f' %data_csr_size + ' MB')
Size of sparse csr_matrix: 4.77 MB
With the use of a sparse matrix, the size of the data in the sparse matrix is just about 5MB, a huge reduction in space. This is mainly due efficient data structure to store only the non-zero elements.
Reference:
1 Comment
[…] vectorizing the corpus by the function, a sparse matrix is […]